Skip to content

Specification Curve Analysis

Motivation

More often than not, empirical researchers need to argue that their chosen model specification reigns. If not, they need to run a battery of tests on alternative specifications and report them. The problem is, researchers can fit a few tables each with a few models in the paper at best, and it's extremely hard for readers to know whether the reported results are being cherry-picked.

So, why not run all possible model specifications and find a concise way to report them all?

The Specification Curve

The idea of specification curve is a direct answer to the question provided by Simonsohn, Simmons and Nelson (2020).1 2

To intuitively explain this concept, below is the Figure 2 from my paper Organization Capital and Executive Performance Incentives on the Journal of Banking & Finance,3 which is used to show the robustness of an substitution effect of organization capital on executive pay-for-performance sensitivity. Therefore, the estimated coefficients for the variable of interest OC are expected to be negative across different model specifications.

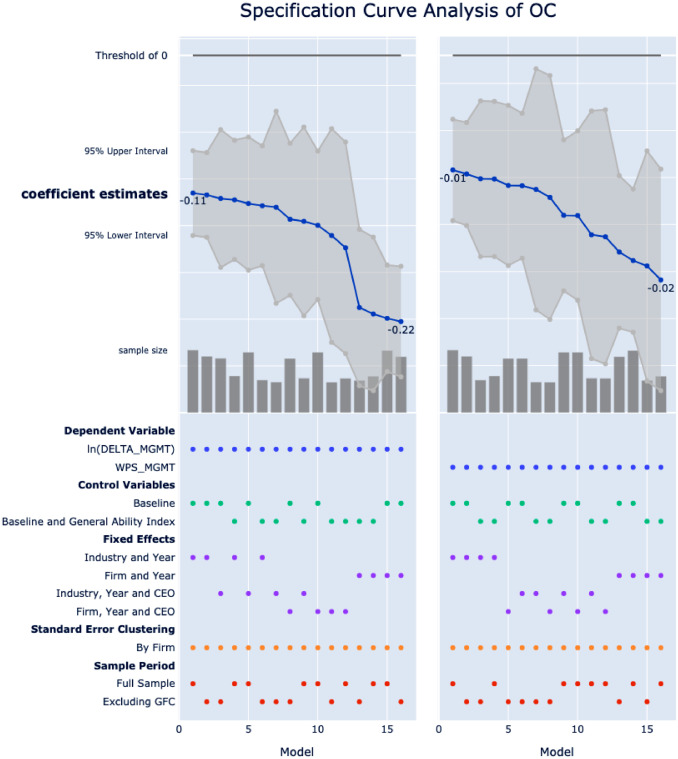
specurve-of-oc

The plot is made up of two parts. The upper panel plots the coefficient estimates of OC in various model specifications, in descending order, and the associated 95% confidence intervals. Sample sizes of each model are plotted as bars at the bottom of the upper panel. For simplicity, we annotate only the maximum and minimum coefficient estimates, as well as the threshold of zero. The lower panel reports the exact specification for each model, where colored dots indicate the choices from various specification alternatives. Both panels share the same x-axis of model number.

To interpret this specification curve, for example, OC has an estimated coefficient of −0.11 in the first model, which uses the natural logarithm of DELTA_MGMT (a measure of executive pay-for-performance sensitivity) as the dependent variable, and control variables as in the baseline model, including industry fixed effects and year fixed effects, clustering standard errors at the firm level, and is estimated on the full sample.

Further, the ordered nature of the curve implies that this is the minimum estimated impact of OC on ln(DELTA_MGMT), whereas the maximum estimated coefficient is doubled at −0.22 when the industry fixed effects are replaced with the more conservative firm fixed effects and estimated on the sample excluding global financial crisis period. More importantly, in all specifications, we find the coefficient estimates of OC to be statistically significant. Using an alternative measure of executive pay-for-performance sensitivity as the dependent variable, again, has minimal impact on the documented substitution effect of OC.

This specification curve reports a total of 2*2*4*1*2=32 specifications:

  • 2 choices of dependent variables (as alternative measures of executive pay-for-performance sensitivity)
  • 2 choices of controls variables (controlling for managerial ability at the cost of reduced sample size)
  • 4 choices of fixed effects
  • 1 choice of standard error clustering
  • 2 choices of sample periods

Beyond reporting all estimates from hundreds and thousands of models, the more appealing point of specification curve is that we can identify the most impactful factors in specifying the model. As the models are sorted by the coefficient estimates, the distribution of dots in the lower panel can reveal whether certain specification choices drive the results.

  • Alternative measures of executive pay-for-performance sensitivity do not affect the main findings.
  • The inclusion of additional control variable of managerial ability does not affect the main findings.
  • The industry and year fixed effects seem to lead to weaker coefficient estimates for the variable of interest, albeit the more conservative firm and year fixed effects lead to stronger ones. This is very important.
  • The main findings hold with and without the global financial crisis (GFC) period.

Of course, even 32 models cannot exhaust all possible specifications. Nevertheless, by addressing the most critical ones, we are able to use one specification curve plot to convince readers that our findings are robust.

specurve - Stata command for specification curve analysis

I developed a Stata command specurve for specification curve analysis. It is written in Stata Mata and has no external dependencies.4 The source code is available at GitHub.

Installation

Run the following command in Stata:

net install specurve, from("https://raw.githubusercontent.com/mgao6767/specurve/master") replace

Example usage & output

Regressions with reghdfe

. use "http://www.stata-press.com/data/r13/nlswork.dta", clear
(National Longitudinal Survey.  Young Women 14-26 years of age in 1968)

. copy "https://mingze-gao.com/specurve/example_config_nlswork_reghdfe.yml" ., replace

. specurve using example_config_nlswork_reghdfe.yml, saving(specurve_demo)

example_reghdfe

IV regressions with ivreghdfe

. copy "https://mingze-gao.com/specurve/example_config_nlswork_ivreghdfe.yml" ., replace
. specurve using example_config_nlswork_ivreghdfe.yml, cmd(ivreghdfe) rounding(0.01) title("IV regression with ivreghdfe")

example_ivreghdfe

Check help specurve in Stata for a step-by-step guide.

Post estimation

Estimation results are saved in the frame named "specurve".

Use frame change specurve to check the results.

Use frame change default to switch back to the original dataset.

  1. Simonsohn, Uri and Simmons, Joseph P. and Nelson, Leif D., 2020, Specification Curve Analysis, Nature Human Behaviour. ↩

  2. Special thanks to Rawley Heimer from Boston College who visited our discipline in 2019 and introduced the Specification Curve Analysis to us in the seminar on research methods. ↩

  3. This plot was made using a previous version of specurve. ↩

  4. Previous versions depend on Stata 16's Python integration. ↩

Comments