AFIN8003 Week 13 - Review

Banking and Financial Intermediation

Dr. Mingze Gao

Department of Applied Finance

2025-06-05

Course overview

About this course

Course description:

• This unit applies finance theory to the context of operational decision-making and risk management in banking and financial intermediation.
• The major decision areas for banking management are covered within a regulatory and corporate responsibility framework.
• Major risks of banks and financial intermediation are being examined.

Key approaches:

• Research-informed teaching.
• Australian focus with global evidence.
• Priority on bank risk management.

Weekly topics

1. Introduction to banking and financial intermediation
2. Risks and regulation
3. Capital management and adequacy
4. Interest rate risk
5. Market risk (guest lecture)
6. Credit risk I: individual loan risk
7. Credit risk II: loan portfolio and concentration risk
8. Liquidity risk
9. Liability and liquidity management (guest lecture)
10. Sovereign risk, foreign exchange risk, and off-balance-sheet risk
11. Loan sales and securitisation
12. Emerging topics in bank risk management
13. Review

The specialness of bank and financial intermediaries

Financial intermediation

A financial system encompasses various financial intermediaries, markets, regulators, and infrastructure in the generation and distribution of financial resources.

Financial intermediation is part of the financial system.

• It is the process by which financial intermediaries, such as banks, facilitate the flow of funds between savers and borrowers.
• Banks are a major part of financial intermediation.

Why is banking and financial intermediation necessary?

A banking analogue of the Modigliani and Miller (1958) theorem would imply that banks are useless with perfect financial markets.

• In a competitive equilibrium, banks make zero profit and have no impact on other agents’ decisions. Firms are indifferent between bank credit and bonds. (Freixas and Rochet 2023)

The existence of banks (and other financial intermediaries) must be justified by their roles in mitigating market frictions.

• A simple look at the Diamond and Dybvig (1983) model.
• The optimal allocation can be achieved with competitive banks offering deposit contracts and investing in the long-term (i.e., maturity transformation).
  • also, asset transformation, risk transformation and liquidity transformation.
  • Panic-based bank runs may occur even when illiquid assets are risk-free.
• Banks are also better positioned to mitigate informational frictions in the market due to economies of scale.
  • Screening costs in the context of adverse selection (Broecker 1990).
  • Monitoring costs in the context of moral hazard (Holmstrom and Tirole 1997).

Risks and regulation

Banking regulations

Failure of banks has significant negative externality. As a result, banks are heavily regulated.

• Loss of deposits for savers
• No credit supply for borrowers
• Impact on real economy
• Global Financial Crisis (GFC) 2007-2009

Broadly, banking regulations can be classified into two aspects:

• Microprudential regulations: safety and soundness of individual institutions
• Macroprudential regulations: stability of the financial system

The two aspects are not mutually exclusive, but complementary.

The banking regulatory landscape

Before GFC, the banking regulations primarily focused on prudential regulations concerning the risks of individual banks.

• Capital adequacy: sufficient capital to cover potential losses.
• Risk management: ability to manage various risks such as credit, market, and operational risks.
• Liquidity management: enough liquid resources to meet immediate obligations.

Post-GFC, the banking regulations have expanded to include macroprudential regulations.

• Systemic focus: greater emphasis on understanding and mitigating systemic risks that could destabilize the entire financial system.
• Countercyclical policies: measures introduced to mitigate the procyclical effects of previous regulatory approaches.
• Stress testing: system-wide tests to assess the resilience of the financial system to shocks.

Bank risks - our approach

In this course, we examine bank risks one by one in a three-step framework:

1. Identify: definition, source and nature
2. Measure: ways to gauge the exposure
3. Manage: strategies to mitigate

Capital management and adequacy

Capital management and regulation

In summary,

• capital is useful to absorb losses and to mitigate insolvency risk;
• regulators determine the adequate capital requirements for FIs.

As a result, FI’s capital is guided by two key factors:

1. regulated capital adequacy requirements, and
2. the risk-return trade-offs.

Who determines the capital requirements?

Actual capital ratios applied can be country-specific, determined by national regulators. However, the Basel Accords provide the global framework for these capital ratios.

• The Basel Committee on Banking Supervision (BCBS) of the BIS sets out the 1988 Basel Capital Accord.
• Member countries of the BIS agreed and implemented the Basel Capital Accord (Basel I).
• A series of updates led to the Basel Accord of 2006 (Basel II)
• Basel III: responding to the 2007-09 financial crisis.

Basel I

Two capital ratios:

1. Tier 1 Capital Ratio
   • Primarily composed of common equity, retained earnings, and disclosed reserves, less goodwill and other intangibles.
   • Calculation: Tier 1 Capital / Risk-Weighted Assets (RWA)
   • Minimum requirement: 4%
2. Total Capital Ratio
   • Minimum requirement: 8%

Features:

• Basel I introduced the systematic measurement of capital adequacy through the use of risk-weighted assets.
• Basel I utilized RWA to account for the varying risk levels of different asset classes, including both on-balance-sheet and off-balance-sheet exposures.

Criticisms:

• Credit Risk Focus: Basel I primarily recognized credit risk in the calculation of risk-weighted assets. It did not initially incorporate market risk or operational risk, leading to criticisms that it did not fully address the spectrum of risks faced by banks.¹

1. A revision in 1998 incorporated market risk into the framework.

Basel II

Basel II comprised three pillars:

1. minimum capital requirements, which sought to develop and expand the standardised rules set out in the 1988 Accord
2. supervisory review of an institution’s capital adequacy and internal assessment process
3. effective use of disclosure as a lever to strengthen market discipline and encourage sound banking practices

• The measurement of capital did not change markedly in Basel II.
• The measurement of risk was significantly enhanced to include operational risk, some market risks in the banking book, and risks associated with securitisation.

Under Basel II, two options are allowed for banks to measure their credit risk:

1. Standardized approach. Similar to Basel I, but more risk-sensitive.
2. Internal ratings-based (IRB) approach. Banks can use their internal rating system or credit scoring models to assess their portfolios, subject to regulatory approval.

Three options are available for measuring operational risk:

1. basic indicator.
2. standardized approach.
3. advanced measurement approach.

GFC and Basel 2.5

The Global Financial Crisis (GFC) in 2007-09 revealed that Basel II was flawed. For example,

• credit ratings of complex securities were conducted by private companies without regulatory supervision or review
• Basel II capital adequacy formula was procyclical, meaning that the required capital was increasing as the crisis unfolded, making it even harder for banks during crisis

In response, Basel 2.5 was passed in 2009 (effective in 2013) and Basel III was passed in 2010 (phased in between 2013 and 2019).¹

• Basel 2.5 updated capital requirements on market risk from banks’ trading activities.

1. Basel III framework was revised and finalized in 2017 and the implementation was extended to January 1, 2022.

Basel III

Basel III is broader in perspective than just a revision of capital, capital adequacy, risk measurement and supervision. It introduced macroprudential measures, targeting the protection of the whole financial system.

Three pillars similar to in Basel II, but with significant enhancements.

1. Improvements to both standardized and IRB approaches in calculating adequate capital.
2. Inclusion of new capital conversion buffer and countercyclical capital buffer to the minimum required capital level.
3. Introduction of two minimum standards for funding liquidity: liquidity coverage ratio and net stable funding ratio.¹
4. Higher capital requirements for trading and derivative activities.
5. Enhanced bank governance.
6. Enhanced risk disclosure.

Note

Basel III is our focus, of course.

1. These liquidity ratios are discussed in Week 10 Liability and Liquidity Management.

Risk-based capital ratio

Under Basel III, depositary institutions (DIs) calculate and monitor four capital ratios:

1. Common equity Tier 1 (CET1) risk-based capital ratio \[ \text{CET1 capital ratio} = \frac{\text{CET1 capital}}{\text{Risk-weighted assets}} \qquad(1)\]

2. Tier 1 risk-based capital ratio \[ \text{Tier 1 capital ratio} = \frac{\text{Tier 1 capital}}{\text{Risk-weighted assets}} \qquad(2)\]

3. Total risk-based capital ratio \[ \text{Total capital ratio} = \frac{\text{Total capital}}{\text{Risk-weighted assets}} \qquad(3)\]

4. Tier 1 leverage ratio \[ \text{Tier 1 leverage ratio} = \frac{\text{Tier 1 capital}}{\text{Total exposure}} \qquad(4)\]

• The calculation of these capital ratios is complex.
• Use risk-weighted assets (RWA) to distinguish the different credit risks of different assets.
• Measure a DI’s credit risk (on-and off-balance-sheet).

Important

• Additional capital charges for market risk and operational risk.
  • For now, we do not consider these risks and their impact on RWA.
  • We briefly explain how they affect RWA and capital ratios at the end of this lecture.

Standardized and IRB approaches for credit risk

Since Basel II, two options are available for banks to measure credit risk for calculating capital requirements.

1. The standardized approach.
   • Used by smaller depositary institutions.
2. The internal ratings-based (IRB) approach.
   • Used by large depositary institutions.
     • US: about 20 of the largest banking institutions with consolidated assets of $250 billion or more.¹
     • Australia: currently approved for use by 6 of the largest banks in Australia.

1. Or with consolidated on-balance-sheet foreign exposures of $10 billion or more.

Type of capital: CET1 Capital

CET1 is the primary or core capital of a DI.

• Common shares
• Share premium resulting from the issue of CET1 instruments
• Retained earnings
• Accumulated and other comprehensive income
• Other disclosed reserves
• Certain minority interests
• Regulatory adjustment applied in the calculation of CET1 Capital.

Type of capital: Tier 1 Capital

Tier 1 Capital is the sum of CET1 Capital and Additional Tier 1 Capital.

Additional Tier 1 Capital:

• Instruments issued by a DI that qualify for Additional Tier 1 Capital and are not included in CET1 capital.¹
• Share premium resulting from the issue of instruments included in Additional Tier 1 Capital.²
• Tier 1 minority interest not included CET1 capital.
• Regulatory adjustments applied in the calculation of Additional Tier I Capital.

1. For example, noncumulative perpetual preferred stock.

2. In Table 21-3 of the textbook Saunders, Cornett, and Erhemjamts (2023), this entry incorrectly reads “Stock surplus (share premium) resulting from the issue of instruments included in Common Equity Tier I”. See page 15 of the original BIS publication “Basel III: A Global Regulatory Framework for More Resilient Banks and Banking Systems”, June 2011.

Type of capital: Total Capital

Total Capital is the sum of Tier 1 and Tier 2 capitals, where Tier 2 Capital is supplementary capital.

Tier 2 Capital:

• Instruments issued by a DI that qualify for Tier 2 Capital and are not included in Tier 1 capital.¹
• Share premium resulting from the issue of instruments included in Tier 2 Capital.²
• Tier 2 minority interest not included Tier 1 capital.
• Certain loan loss provisions.
• Regulatory adjustments applied in the calculation of Tier 2 Capital.

1. It includes secondary “equity-like” capital resources, for example, loan loss reserves and some convertible and subordinated debt instruments.

2. In Table 21-3 of the textbook Saunders, Cornett, and Erhemjamts (2023), this entry incorrectly reads “Stock surplus (share premium) resulting from the issue of instruments included in Tier I capital”. See page 17 of the original BIS publication “Basel III: A Global Regulatory Framework for More Resilient Banks and Banking Systems”, June 2011.

Capital adequacy framework

• Credit risk
  • The risk-based capital ratios as described earlier.
• Interest rate risk
  • No formal add on yet.
• Market risk
  • Additional capital charge.
• Operational risk
  • Additional capital charge.

Minimum required capital adequacy ratios

The minimum required capital ratios: \[ \begin{aligned} \text{CET1 capital ratio} &= \frac{\text{CET1 capital}}{\text{Risk-weighted assets}} \ge 4.5\% \\ \text{Tier 1 capital ratio} &= \frac{\text{Tier 1 capital}}{\text{Risk-weighted assets}} \ge 6\% \\ \text{Total capital ratio} &= \frac{\text{Total capital}}{\text{Risk-weighted assets}} \ge 8\% \\ \text{Tier 1 leverage ratio} &= \frac{\text{Tier 1 capital}}{\text{Total exposure}} \ge 4\% \end{aligned} \qquad(5)\]

Overview of capital ratios calculation

1. Calculate the amount of capital (CET1, Tier 1, Total Capital).
2. Calculate the risk-weighted assets (RWA)¹: sum of the amount of each asset multiplied by a risk weight specific to its riskiness.
   1. On-balance-sheet:
      1. Each asset has a risk weight
      2. Multiply the asset by the corresponding risk weight
   2. Off-balance-sheet:
      1. Convert each asset to an on-balance-sheet equivalent
      2. Multiply the equivalent exposure by the corresponding risk weight
   3. Sum the on-balance-sheet and off-balance-sheet RWA
3. Calculate the capital ratios based on the amount of capital and RWA.

1. On- and off-balance-sheet assets whose values are adjusted for approximate credit risk.

Capital conversion buffer and countercyclical capital buffer (CCyB)

Basel III introduced two buffers, capital conversion buffer and countercyclical capital buffer, to the minimum required capital level.

Capital conversion buffer:

• 2.5% of risk weighted assets comprised of CET1 only
• DI to hold minimum of 7% common equity Tier 1 (minimum of 4.5% plus conservation buffer of 2.5%)
• If a DI’s capital conservation buffer falls below 2.5%, constraints are imposed on the DI’s distributions (e.g. dividends and bonuses)

CCyB:

• May be declared by a country experiencing excess aggregate credit growth
• Vary between 0 and 2.5% of risk-weighted assets comprised of CET1 only
• If a DI’s CCyB falls below the set level, constraints are imposed on the DI’s distributions (e.g. dividends and bonuses)

Risk-based capital: beyond credit risk

So far, the capital ratios (specifically, RWA) are calculated to account for the DI’s credit risk. However, a DI’s insolvency risk can also manifest from interest rate risk, market risk, operational risk, and more.

In Basel III, RWA should be the sum of three components:¹

1. RWA for credit risk (covered in this lecture)
2. RWA for market risk. Can be calculated using two approaches:²
   1. Standardized approach proposed by regulators. Revised standards published in 2016 to be implemented in 2019.
   2. DI’s internal market risk model subject to regulator approval. Move towards expected shortfall rather than value at risk (VaR).
3. RWA for operational risk. Some complicated calculation.³

Important

The RWA in the minimum capital ratios (Equation 5) is the sum of all three RWAs.

We covered only the RWA for credit risk.

1. To date, no formal add on has been required yet (development in progress).

2. For details, see RBC20.9.

3. For details, see RBC20.10.

Interest rate risk

What is interest rate risk?

Interest Rate Risk

Interest rate risk is the possibility of a financial loss due to changes in interest rates.

One of the key functions performed by financial institutions (especially depositary institutions) is maturity transformation. For DIs, they take short-term deposits from depositors and make long-term loans to borrowers. As a result,

1. This maturity transformation means that FIs have mismatches of maturities of their liabilities (e.g., deposits) and assets (e.g., loans).
2. Maturity mismatch exposes FIs to (unexpected) interest rate changes:
   1. refinancing and reinvestment risks
   2. financial instruments have different levels of value sensitivity to interest rate changes
3. Interest rate is volatile and can be unexpected.

Interest rate risk and Basel framework

As discussed previously, the three pillars of Basel framework (since Basel II) include:

1. minimum capital requirements
2. supervisory review
3. effective use of disclosure (for market discipline)

The Pillar 1 involves a capital adequacy framework surrounding minimum ratios of various capital (CET1, Tier 1, Total) to RWA.

• The RWA is sum of RWAs for credit risk, market risk, and operational risk.
• There is currently no “RWA for interest rate risk”.

The Interest Rate Risk in the Banking Book (IRRBB) is part of the Basel capital framework’s Pillar 2 (supervisory review) and Pillar 3 (disclosure).

Repricing model

• Repricing model is also known as the funding gap model.
  • A book value accounting cash flow analysis of the repricing gap between the interest income earned on an FI’s assets and the interest paid on its liabilities over some period.
  • Focus on the changes of net interest income (NII).
• A simple model used by small FIs.
• APRA requires smaller ADIs to use the repricing method to estimate interest rate exposures in their banking book for capital adequacy purposes.

Repricing gap, RSA and RSL

Repricing gap is the difference between rate-sensitive assets (RSA) and rate-sensitive liabilities (RSL).

• RSA: assets whose interest rates will be repriced or changed over some future period (rate-sensitive assets)
• RSL: liabilities whose interest rates will be repriced or changed over some future period (rate-sensitive liabilities)

An asset (or liability) is “rate-sensitive” if it is repriced at or near current market interest rates within a certain time horizon (or maturity bucket). For example,

• a variable-rate mortgage’s interest rate may be reset every quarter based on the prevailing interest rate.
• interest rate of term deposits are also adjusted frequently.

The repricing model

The repricing model can be used to estimate the change in the FI’s net interest income in a particular repricing bucket if interest rates change.

\[ \Delta NII_i = (GAP_i) \times \Delta R_i = (RSA_i - RSL_i) \times \Delta R_i \]

where:

• \(\Delta NII_i\) is the change in net interest income in the \(i\)th bucket.
• \(GAP_i\) is the dollar size of the gap between the book value of RSA and RSL in maturity bucket \(i\).
• \(\Delta R_i\) is the change in the level of interest rates impacting assets and liabilities in the \(i\)th bucket.

Duration model

The essence of duration gap model is the concept of duration, which is covered in introductory finance courses.

Duration directly measures the interest rate sensitivity of an asset or liability:

\[ \frac{\Delta P}{P} = - D \times \frac{\Delta R}{1+R} = - MD \times \Delta R \qquad(6)\]

where

• \(\Delta P\) is the price change of assets or liabilities
• \(\Delta R\) is the change of interest rate
• \(MD\) is the modified duration that equals to \(\frac{D}{1+R}\)

The larger the numerical value of \(D\), the more sensitive is the price of that asset or liability to changes or shocks in interest rates.

Important

The relationship is only true for small changes in the yield.

Duration and interest rate risk management

Duration can be used to measure a financial institution’s duration gap to evaluate the FI’s overall interest rate exposure. It is possible to calculate the duration of the asset portfolio and of the liability portfolio.

• Duration of a portfolio is the weighted average duration of its components.

Duration of assets portfolio:

\[ D_A = \sum_{i=1}^{N_A} w_{iA} \times D^A_i \]

where \(N_A\) is the total number of assets, \(w_{iA}\) is the market value weight of asset \(i\), \(D^A_i\) is the duration of asset \(i\).

So, change of assets value for a given change in interest rate is

\[ \Delta A = - D_A \times A \times \frac{\Delta R}{1+R} \qquad(7)\]

Duration of liabilities portfolio:

\[ D_L = \sum_{i=1}^{N_L} w_{iL} \times D^L_i \]

where \(N_L\) is the total number of liabilities, \(w_{iL}\) is the market value weight of liability \(i\), \(D^L_i\) is the duration of liability \(i\).

So, change of liabilities for a given change in interest rate is

\[ \Delta L = - D_L \times L \times \frac{\Delta R}{1+R} \qquad(8)\]

The duration model

We know that total assets (\(A\)) is the sum of liabilities (\(L\)) and equity (\(E\)): \(A=E+L\).

Therefore, \(E = A - L\), and \(\Delta E = \Delta A - \Delta L\).

Making use of the previous results Equation 7 and Equation 8, we have

\[ \Delta E = \left[- D_A \times A \times \frac{\Delta R}{1+R}\right] - \left[- D_L \times L \times \frac{\Delta R}{1+R}\right] \qquad(9)\]

If the level of interest and expected shock to interest rates are the same for both assets and liabilities, then:

\[ \Delta E = - (D_A - D_L k) \times A \times \frac{\Delta R}{1+R} \qquad(10)\]

where \(k=\frac{L}{A}\) measures the FI’s leverage.

The duration model

Let’s examine the duration model Equation 10:

\[ \Delta E = - (D_A - D_L k) \times A \times \frac{\Delta R}{1+R} \]

The effect of interest rate changes on the market value of an FI’s net worth breaks down into three effects:

1. The leverage-adjusted duration gap: \((D_A-D_L k)\)
2. The size of the FI: \(A\)
3. The size of the interest rate shock: \(\frac{\Delta R}{1+R}\)

Market risk

Market risk

Market Risk

Market risk is uncertainty of an FI’s earnings on its trading portfolio caused by changes, particularly extreme changes, in market conditions such as the price of an asset, interest rates, market volatility, and market liquidity.

FIs are concerned about the potential impact of changing market conditions on their trading book and ultimately their net worth and solvency.

A natural question becomes:

How to quantify such impact? What is the potential change in value of trading portfolio for a given period?

More specifically,

1. What is the worst loss we can expect not to exceed with a given confidence level over a specific time horizon?
2. What is the expected loss when losses exceed a certain level over a specific time horizon?

Answering these questions leads to the development of two important concepts for measuring market risk exposure:

1. Value at Risk (VaR).
2. Expected Shortfall (ES).

We start with the concept of Value at Risk (VaR), then discuss its limitations and the use of Expected Shortfall (ES).

Value at Risk (VaR)

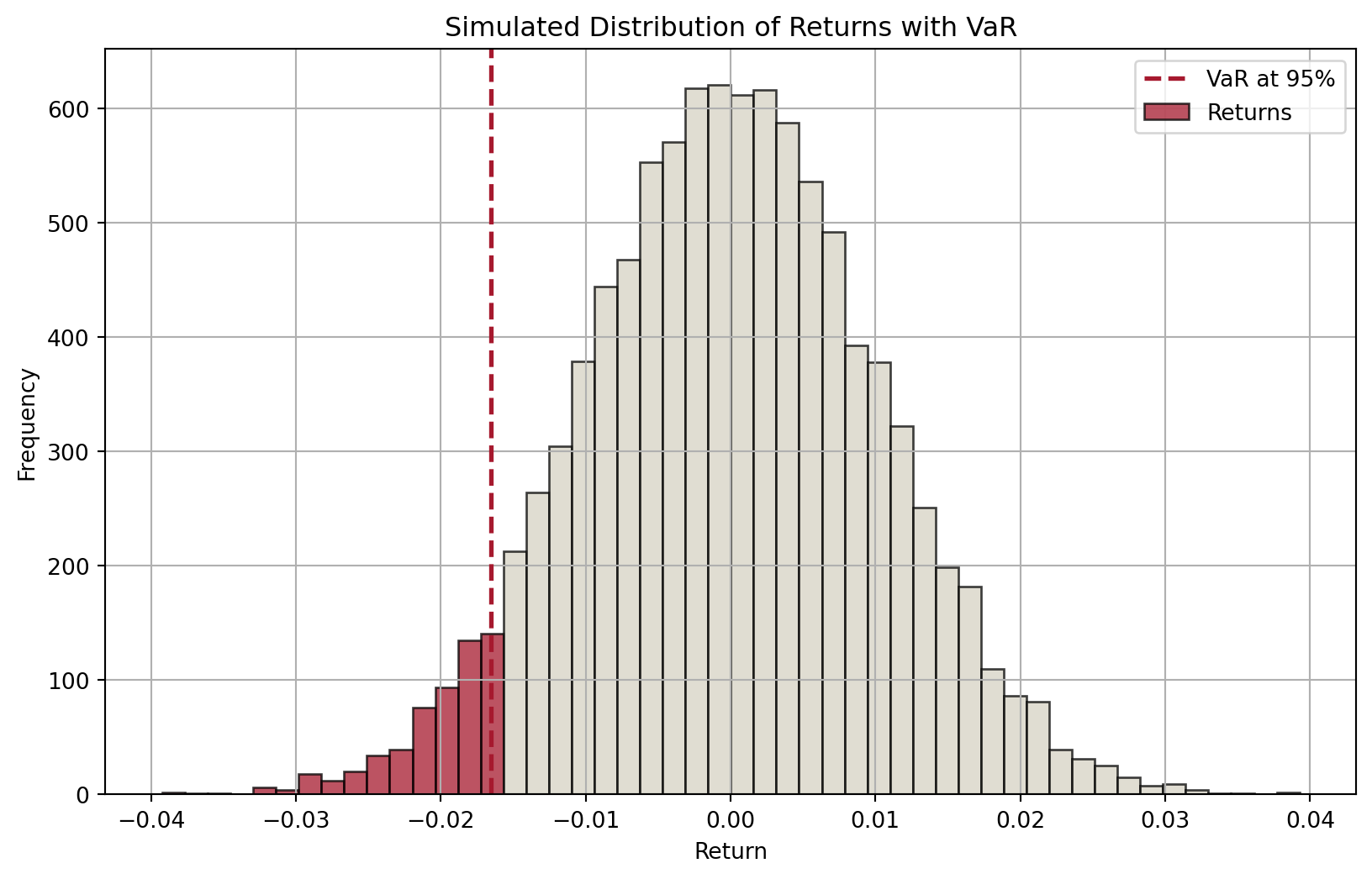
Suppose we know the distribution of an asset’s returns over a specific period (in the future), then for a given confidence level \(c\in[0,1]\) (e.g., \(c=0.95\)), we can partition the distribution into two parts: one (in red) that represents a proportion of \((1-c)\) of the distribution and the other (in blue) accounting the remaining \(c\) proportion.

Figure 1: Distribution of expected returns and VaR

Therefore, the cutoff value of returns that separates the two parts defines:

• a minimum return that we are confident 95% of the time, or
• a maximum loss that we are confident 95% of the time.

Models for computing VaR

Over the years, many models have been developed to compute VaR.

This is because we do not have the return distribution of trading portfolio over a specific period in the future.

• If we do, then VaR is unambiguous.

Therefore, different assumptions lead to different models and approaches. We are interested in three in this course:

1. RiskMetrics (variance-covariance approach)
2. Historic or back simulation
3. Monte Carlo simulation

Expected Shortfall (ES)

The drawbacks of VaR became painfully evident during the financial crisis as asset returns plummeted into the fat-tail region of non-normally shaped distributions.

FI managers and regulators were forced to recognize that VaR projections of possible losses far underestimated actual losses on extreme bad days.

Now, regulators have replaced VaR with the expected shortfall (ES) measure as the main measure of market risk.

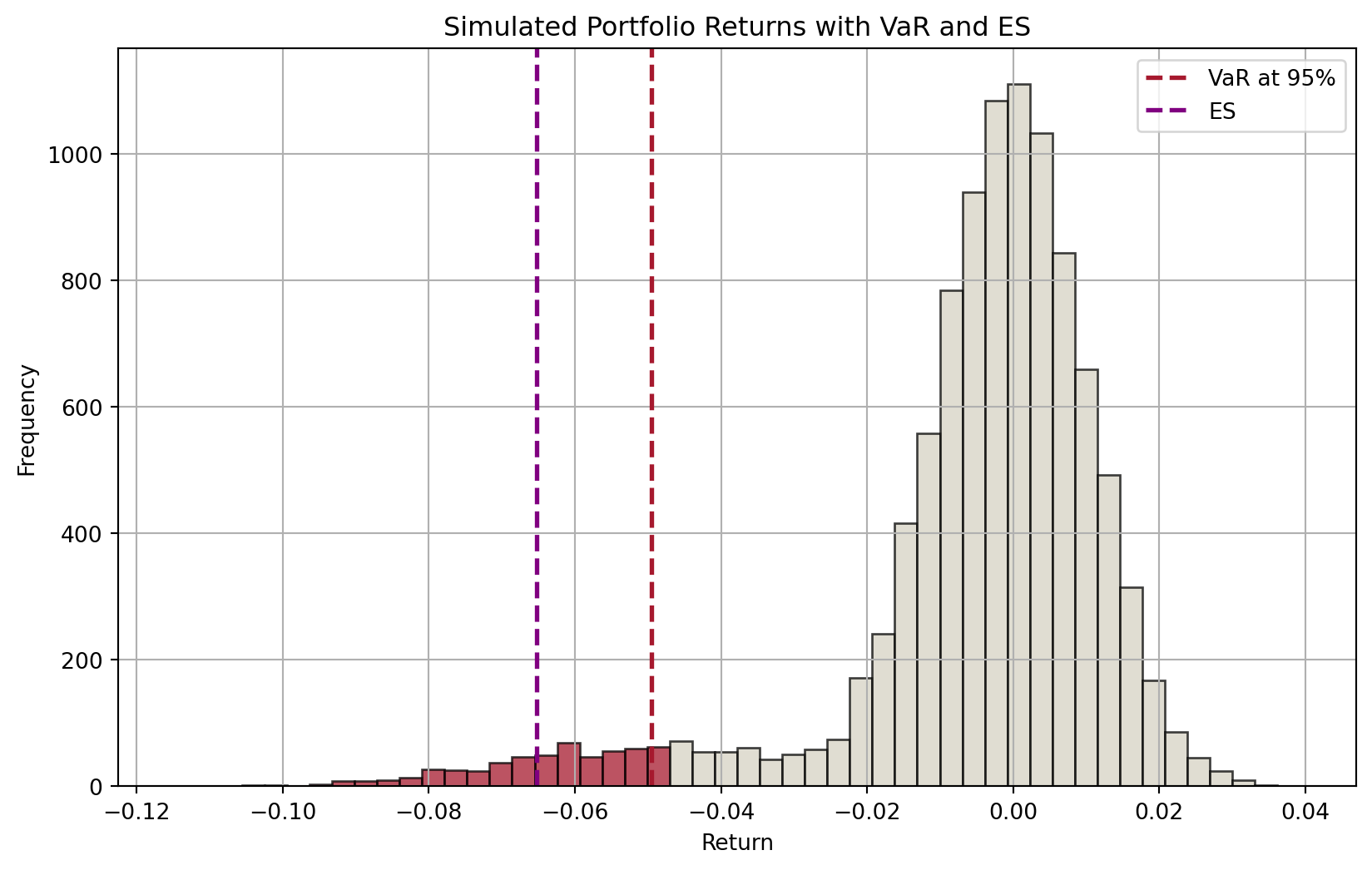
Expected shortfall, aka “conditional VaR”, estimates the expected value of losses beyond a given confidence level—that is, it is the average of VaRs beyond a given confidence level.

ES: definition

For a given confidence level \(c\) and a continuous probability distribution, ES can be calculated as \[ ES(c) = \frac{1}{1-c}\int_c^1 VaR(c)du \]

That is, for a confidence level of, say, 95% (i.e., \(c\)), we measure the area under the probability distribution from the 95th to 100th percentile.

Figure 2: Distribution of expected returns and ES

ES: advantages and (potential) problems

ES is the average of losses that occur beyond the VaR level. It provides a better risk assessment by considering the tail of the loss distribution.

In addition, an important advantage of ES over VaR is that ES is additive.

• This means that the ES of a portfolio equals the sum of individual assets’ ESs.
• The same does not hold true for VaR: recall that we have to consider covariances.

Potential issues with the use of ES include:

• Estimation challenges, model dependency, computational complexity.

Credit Risk I: Individual Loan Risk

Credit risk

As suggested by Table 1 below, credit risk is likely the most significant risk factor, the risk that the promised cash flows from loans and securities may not be paid in full (e.g., borrower defaults).

Table 1: RWA of Australian banks in 2023 (source: Capital IQ)

	CBA	Westpac	NAB	ANZ	Macquarie
RWA for credit risk	362,869	339,758	355,554	349,041	97,485
RWA for market risk	61,968	51,676	38,274	41,967	11,663
RWA for operational risk	43,155	55,175	41,178	42,319	15,828
Other RWA	0	4,809	0	0	0
Total RWA	467,992	451,418	435,006	433,327	124,976

Calculating the return on a loan

Once the decision to make a loan has been made, the pricing of the loan is an important aspect of credit risk management, which includes adjustments for the perceived credit risk of the borrower as well as any fees and collateral backing the loan.

A traditional return on assets approach to calculate the return on a loan is explained here.

Contractually promised return on a loan

Direct and indirect fees and charges:

1. Loan origination fee (\(f\)) for processing the application.
2. Compensating balance requirement (\(b\)) to be held as (demand) deposits.
   • A portion of the loan that the borrower must keep in a deposit account, typically earning little or no interest, which helps the bank secure funds and reduce the effective loan amount while still charging interest on the full loan value.
3. Reserve requirement (\(RR\)) imposed by regulatory authority on the demand deposits.

The gross return on loan (\(k\)) per dollar lent is given by \[ 1+k = 1+\frac{f+(BR+\phi)}{1-[b(1-RR)]} \]

The expected return on a loan

The promised return on a loan (\(k\)) can differ from the expected return and the actual return on the loan because of default risk.

At the time the loan is made, the expected return \(E(r)\) per dollar lent is related to the promised return \(k\) as follows: \[ 1+E(r) = p(1+k) + (1-p)\times 0 \] where \(p\) is the probability of complete repayment of the loan and \((1-p)\) is the probability of default, in which case the FI receives nothing.¹ The expected return is a weighted average of:

• Full repayment: \((1+k)\) with probability of \(p\)
• No repayment: 0 with probability of \((1-p)\)

1. In practice, the FI may recover part of the loan.

Measurement of credit risk

Many different qualitative and quantitative models are employed to assess the default risk on loans and bonds.

• They are not mutually exclusive.
• An FI manager may use both qualitative and quantitative models and use more than one model to reach a credit decision.

Credit scoring models use observed borrower characteristics to

1. either calculate a score representing the applicant’s default probability, or
2. sort borrowers into different default risk classes.

Scoring models might help to:

• Establish factors that help to explain default risk
• Evaluate the relative importance of these factors
• Improve the pricing of default risk
• Sort out bad loan applicants
• More easily calculate reserve needs

Three broad types

1. Linear probability models
2. Logit models
3. Linear discriminant analysis

RAROC

Risk-adjusted return on capital (RAROC) was pioneered by Bankers Trust (acquired by Deutsche bank in 1998).

\[ RAROC = \frac{\text{One-year net income on a loan}}{\text{Loan risk}} \] where \[ \text{One-year net income on loan} = (\text{Spread} + \text{Fees}) \times \text{Dollar value of the loan outstanding} \] and Loan risk can be measure by, for example, duration. \[ \frac{\Delta LN}{LN} = - D_{LN} \frac{\Delta R}{1+R} \] so that \[ \underbrace{\Delta LN}_{\text{dollar risk exposure}} = - \underbrace{D_{LN}}_{\text{duration of loan}} \times \underbrace{LN}_{\text{loan amount}} \times \underbrace{\frac{\Delta R}{1+R}}_{\text{shock}} \]

• Loan approval if RAROC > benchmark return on capital.

Option models of default risk

Rationale:

• A borrower borrows to invest.
• If its investments are successful, the borrower repays.
• If its investments fail and the borrower cannot repay the lender,
  • The borrower has an option to default on its debt, simply turning any remaining assets over to the lender.
• The borrower’s (equity holders’) loss is capped due to limited liability.

Note

The KMV Corporation¹ turned this relatively simple idea into a credit monitoring model.

Many of the largest U.S. FIs are now using this model to determine the expected default frequency (EDF) of large corporations.

1. The KMV Corporation was purchased by Moody’s in 2002 and is now part of Moody’s Analytics Enterprise Risk Solutions.

Credit Risk II: Loan Portfolio and Concentration Risk

Simple models

• Regulations are in place to limit such exposure.
• As a result, individual loans rarely cause material losses or bank failures.
• Primary cause of credit-related distress is that pools of individual loans sharing similar characteristics perform similarly, especially during extreme conditions.
• An important lesson learned is that products exposed to the same types of risks can have different names and under different business units.

Two simple models widely employed to measure credit risk concentration in the loan portfolio:

1. Migration analysis
2. Concentration limits

Loan portfolio diversification and MPT

MPT can be used to measure and control an FI’s aggregate credit risk exposure.

Any model that seeks to estimate an efficient frontier for loans needs to determine and measure three things:

• The expected return on individual loans
• The risk of individual loans
• The correlation of default risks between loans

The fundamental lesson of MPT is that by taking advantage of its size, an FI can diversify considerable amounts of credit risk as long as the returns on different assets are imperfectly correlated with respect to their default risk adjusted returns.

Moody’s Analytics RiskFrontier Model

Moody’s Analytics RiskFrontier model (previously Portfolio Manager model) estimates the return, risk and correlations between loans in an FI’s loan portfolio (with its own proprietary methods), which are then incorporated into the standard MPT equations to get an estimate of the risk and return of the FI’s loan portfolio.

1. Moody’s Analytics Credit Monitor model estimates EDF (Expected Default Frequency) to examine the default risk of individual loans.
2. Moody’s Analytics RiskFrontier model then uses EDF to identify the overall risk of the loan portfolio.
   • Does not require loan returns to be normally distributed
   • Applies MPT to the loan portfolio, although many loans have non-traded aspects

Moody’s Analytics RiskFrontier Model (cont’d)

In Moody’s Analytics RiskFrontier model, portfolio return and risk are a function of:

• the extent to which loan (exposure) values can change over a one-year horizon, and
  • based on EDF and the loss given default (LGD)
• how these value changes move together across different loans in the loan portfolio (correlations).
  • based on the joint impact of close to 1,000 different systematic factors, which reflect the global economy, region, industry, and country

Moody’s Analytics RiskFrontier Model (cont’d)

Required input variables:

1. \(R_i\): Expected return on a loan to a borrower \(i\) is the loan’s all-in-drawn spread (\(AIS\)) minus expected loss (expected default frequency times loss given default (LGD)).¹ \[ R_i = AIS_i - E(L_i) = AIS_i - (EDF_i\times LGD_i) \]
   • The Basel Committee assessed a fixed 45% LGD on secured loans if fully secured by physical, non–real estate collateral and 40% if fully secured by receivables.

2. \(\sigma_i\): Risk of a loan to borrower \(i\), “unexpected loss”, is the volatility of the loan’s default rate \(\sigma_{D_i}\) times the amount lost given default (LGD).² \[ \sigma_i = UL_i = \sigma_{D_i} \times LGD_i = \sqrt{EDF_i(1-EDF_i)} \times LGD_i \]
   • Assume defaults are binomially distributed (default or not), the standard deviation of default rate (\(\sigma_{D_i}\)) is \(\sqrt{EDF_i(1-EDF_i)}\).

3. \(\rho_{ij}\): Correlation of default risks between borrowers \(i\) and \(j\) is the correlation between the systematic return components of the asset returns of \(i\) and \(j\).

To measure the unobservable default risk correlation between any two borrowers, the Moody’s Analytics Global Correlation Model (GCORR) uses the systematic asset return components of the two borrowers and calculates a correlation that is based on a factor model rather than direct historical observations.

1. In the textbook Saunders, Cornett, and Erhemjamts (2023), this equation has a typo: \(E(L_i)\) is written as \(R(L_i)\). Note that \(E(\cdot)\) represents the “expectation” sign and \(L_i\) stands for loan loss.

2. In the textbook Saunders, Cornett, and Erhemjamts (2023), this equation is entirely incorrectly written.

Use of derivatives to manage credit risk

• Diversification of loan portfolio helps FIs to manage their credit risk exposure.
• New types of derivative instruments are now available to better allow FIs to hedge their credit risk both on individual loans or on loan portfolios.
  • Credit forwards, options, and swaps.
• These credit derivatives allow FIs to separate the credit risk exposure from the lending process itself.

Credit (default) swaps (CDS)

Fastest-growing types of swaps. Most important type of credit derivatives.

Why CDS?

1. Credit risk is still more likely to cause an FI to fail than is either interest rate risk or FX risk.
2. CDSs allow FIs to maintain long-term customer lending relationships without bearing the full credit risk exposure from those relationships.

We examine two types of credit swaps:

1. total return swap
2. pure credit swap

Liquidity Risk

Liquidity risk

Liquidity risk is a normal aspect of everyday management of a financial institution (FI). It can arise on both sides of the balance sheet:

• Liability side
  • Depositors and other claim holders decide to cash in their financial claims immediately
    • The DI has to borrow additional funds or sell assets
  • DI need to be able to predict the distribution of net deposit drains
    • The difference between deposit withdrawals and deposit additions on any specific normal banking day

• Asset side
  • Risk from OBS loan commitments and other credit lines
  • Change of the value of investment securities portfolios due to unexpected changes of interest rates
  • Problems associated with ‘quick’ asset sales/fire-sales
    • High costs for turning illiquid assets into cash
    • Low sales price; in worst case, fire-sale price

Purchased liquidity management

• A DI manager seeking to purchase liquidity turns to markets for purchased funds.
• Options include the cash market and the repurchase agreement markets, which are interbank markets for short-term loans.
• Alternatively, the DI manager could:
  • Issue additional wholesale certificates of deposit.
  • Sell notes and bonds.
• Borrowed funds (at market rates) are likely to be at higher rates than interest paid on deposits.

Stored liquidity management

• A DI manager could also liquidate some of its assets, utilizing its stored liquidity.

• Traditionally, U.S. DIs hold cash reserves at the Federal Reserve and in their vaults to meet liquidity needs.

• The Federal Reserve sets minimum reserve requirements for banks’ cash reserves.

• Despite these requirements, DIs often hold cash reserves above the minimum to manage liquidity drains.

Note

• In U.S., the Fed reduced the reserve requirement to 0, effective March 26, 2020.
• In Australia, the RBA does not impose formal reserve requirements.

Liquidity risk measures

• During the financial crisis, many DIs struggled to maintain adequate liquidity.
• Central banks had to provide extraordinary levels of liquidity assistance to sustain the financial system.
• Despite this support, some DIs failed or were forced into mergers.
• In response, the BIS’s Basel Committee on Banking Supervision introduced two new regulatory standards for liquidity risk supervision:
  • Liquidity Coverage Ratio (LCR):
    • Came into effect on January 1, 2015.
    • Gradually implemented, reaching full compliance on January 1, 2019.
  • Net Stable Funding Ratio (NSFR):
    • Became a minimum standard on January 1, 2018.
• These rules apply to:
  • Large, internationally active banking organizations with $250 billion or more in total consolidated assets.
  • Organizations with $10 billion or more in total on-balance-sheet foreign exposure.
  • Consolidated subsidiary depository institutions with $10 billion or more in total assets.

Liquidity Coverage Ratio (LCR)

• The Liquidity Coverage Ratio (LCR) is designed to ensure that a DI maintains sufficient high-quality liquid assets (HQLA).
• These HQLA must be easily convertible to cash to meet liquidity needs over a 30-day period.
• The LCR is based on an “acute liquidity stress scenario” defined by supervisors.
  • The scenario includes both institution-specific and systemic shocks.
  • It reflects actual conditions experienced during the global financial crisis.
• The purpose of maintaining the LCR is to ensure that DIs can survive severe liquidity stress for at least 30 days.
• The LCR is reported to DI supervisors on a monthly basis.

\[ \text{Minimum LCR} = \frac{\text{Stock of HQLAs}}{\text{Total net cash outflows over next 30 calendar days}} \ge 100\% \]

Liquidity Coverage Ratio (LCR) (cont’d)

The stock of HQLAs is defined as follows:

• Liquid assets in the stock must remain liquid in times of stress (i.e., convertible into cash at little loss of value and can be used at the central bank discount window as collateral).
• Liquid assets in the stock must be “unencumbered”, i.e., free of legal, regulatory, contractual, or other restrictions on the ability of the bank to liquidate, sell, transfer, or assign the asset.
• Liquid assets in the stock are divided into level 1 and level 2. Level 1 amount has no cap, and level 2 amount is capped at 40 percent of the stock.
  • Level 1 assets are limited to:
    • Cash, central bank reserves, marketable securities representing claims on or guaranteed by sovereigns, central banks, public sector entities (PSE), and some supranational institutions (e.g., BIS, IMF, ECB, multilateral development banks).¹
  • Level 2A assets (15% haircut):
    • Eligible marketable securities representing claims on or guaranteed by sovereigns, central banks, PSEs, or multilateral development banks.
    • Eligible corporate debt securities and covered bonds.
  • Level 2B assets:
    • Eligible residential mortgage backed securities (25% haircut).
    • Eligible corporate debt securities and equities (50% haircut).

1. There’re more restrictions.

Liquidity Coverage Ratio (LCR) (cont’d)

The total net cash outflows is defined as:

\[ \text{Total net cash outflows over next 30 calendar days} = Out - \min(In, 75\% \times Out) \]

where

• \(Out\) is total expected cash outflows
• \(In\) is total expected cash inflows

Cash inflows and outflows are computed based on the type of assets/liabilities and associated draw-down factors.

Note

For a detailed calculation of cash outflows and inflows, refer to textbook Saunders, Cornett, and Erhemjamts (2023) or to the suggested readings.

Net Stable Funding Ratio (NSFR)

• The Net Stable Funding Ratio (NSFR) focuses on long-term liquidity management on a DI’s balance sheet.
• It evaluates liquidity across the entire balance sheet, encouraging the use of stable sources of financing.
• The NSFR requires a minimum amount of stable funding over a one-year time horizon.
  • It aims to limit the reliance on short-term wholesale funding, a significant issue during the financial crisis.
• The NSFR has been reported to DI supervisors quarterly since 2018.

\[ \text{NSFR} = \frac{\text{Available amount of stable funding}}{\text{Required amount of stable funding}} \ge 100\% \]

Net Stable Funding Ratio (NSFR)

Available stable funding (ASF) includes:

• Bank capital
• Preferred stock with a maturity > 1 year
• Liabilities with maturities > 1 year
• The portion of retail deposits and wholesale deposit expected to stay with bank during a period of idiosyncratic stress

These equity and liabilities are assigned to one of five categories, each with a specific ASF factor. ASF is calculated as the sum of the weighted amounts.

Required stable funding (RSF) is calculated as the sum of

1. the value of the on-balance-sheet assets multiplied by a specific RSF factor assigned to each particular asset type, and
2. the amount of off-balance-sheet (OBS) activities (or potential liquidity exposure) multiplied by the associated RSF factor.

Liquidity risk, unexpected deposit drains, and bank runs

Major liquidity problems can arise, however, if deposit drains are abnormally large and unexpected, which may occur for a number of reasons, including:

• Concerns about a DI’s solvency relative to those of other DIs.
• Failure of a related DI (the contagion effect).
• Sudden changes in investor preferences regarding holding nonbank financial assets (such as T-bills or mutual fund shares) relative to deposits.

In these cases, unexpected deposit drains could trigger a bank run that may eventually force a bank into insolvency.

In the worst case, a bank panic may occur - systemic or contagious bank run on deposits of banking industry.

Bank runs, the discount window, and deposit insurance

The two major liquidity risk insulation devices are deposit insurance and the discount window.

1. Deposit insurance
2. Discount window:
   • A facility provided by central banks where FIs can borrow short-term funds to meet liquidity needs, typically at an interest rate called the “discount rate.”
   • During the March 2023 United States bank failures, banks drew $153 billion from the discount window as of 15 March 2023, a new record.

Not without economic costs

• Protection may encourage DIs to increase liquidity risk

Liability and Liquidity Management

Source of liquidity

Historically, primary method of meeting cash demands: asset liquidity (stored liquidity)

• Examples: cash, treasury securities
• Stock of liquid assets in an FI depends on
  • FI’s willingness to trade off liquidity and returns
  • FI’s ability to use liability liquidity

Today, primary method of meeting cash demands: liability liquidity / management (purchased liquidity)

• Examples: interbank market for exchange settled funds, repos, interbank market

Asset-side liquidity and management

• Liquid assets, e.g., Treasury notes/bonds, are traded in a deep market¹

• The composition of an FI’s liquid asset portfolio (especially cash and government securities) is partly determined by:
  • minimum liquid-asset reserve requirements imposed by the central bank
  • earnings consideration
• Government securities act as secondary buffer reserves
  • When significant drains on cash reserves occur, these securities can be turned into cash quickly and with very little loss of principal value because of the deep nature of the markets in which these assets are traded.

1. A market is deep when even large trading volumes will not impact on price.

Risk-return trade-off for liquid assets

• Liquid assets carry a comparatively lower interest rate
• At the heart of management of the liquid asset portfolio is balancing the benefits and costs of holding liquid assets
  • Cash immediacy versus reduced return
• Need to consider, among other things, the variability of deposit inflows and outflows, the yield and liquidation costs of non-liquid assets, the interest paid on purchased funds in the money market, and more
• Day-to-day liquidity management means that a DI faces the risk of either undershooting or overshooting the required liquidity requirement on any given day.
  • Undershooting the regulatory required liquidity ratios (e.g., LCR, NSFR) may involve specified additional charges.
  • Holding cash reserves in excess of the minimum required can be costly.¹
• The management of a DI’s exchange settlement account (ESA) at the RBA is critical.

Note

ESA is an account held at the Reserve Bank of Australia by financial institutions to settle financial obligations arising from the clearing of payments.

1. RBA pays ‘cash target rate minus 10 basis points’ interest on ESA balances.

The cash market and Exchange Settlement Account (ESA)

The cash market is where banks lend and borrow funds from each other, typically on an overnight basis. These funds can be used to:

• Meet liquidity needs: Banks may borrow funds to ensure they meet short-term liquidity requirements, such as the ESA balances.
• Support lending activities: Banks may also use borrowed funds to support ongoing lending activities.
• Facilitate settlement of transactions: The funds can help banks settle large-scale interbank transactions efficiently.

Importantly,

• The price of funds in this market is the interest rate on these interbank loans, which is called the cash rate in Australia.
• The quantity traded in this market is called the Exchange Settlement (ES) balance - the balance of DI’s deposit accounts at the RBA, the ESA.

The cash market, ESA, and repo transactions

RBA sets a target for the cash rate, it is often referred to as a “tool” of monetary policy.

Prior to the COVID-19 recession,

• the cash rate target was the RBA’s only active monetary policy tool.
• the RBA managed the supply of ES balances so that it met estimated demand and the cash rate was close to its target.
• the RBA achieved cash rate target through open market operations, particularly through repurchase agreements (repos).

Repo transactions of RBA

A repo is a transaction with two parts.

• In the first part, the Reserve Bank could lend ES balances to a bank and receive a bond in exchange. This increases the supply of ES balances available to banks.
• In the pre-arranged second part, the transaction is reversed. The Reserve Bank returns the bond and receives back the ES balances, which decreases the supply of ES balances.

After the introduction of the package of policy measures in response to the COVID-19 recession,

• ES balances substantially increased.
• the RBA, as a result, no longer conducts daily open market operations to manage ES balances.

The new dynamics

Since COVID-19, the RBA significantly adjusted its monetary operations, moving away from repos as the primary tool for managing liquidity. Banks now manage their ESA balances primarily through other mechanisms:

• Term Funding Facility (ended 30 June 2024): Introduced during the pandemic, the TFF allowed banks to access longer-term funding at very low rates. It helped banks manage funding needs over the pandemic period.
• Government Bond Purchases (ceased on 10 February 2022): The RBA engaged in large-scale government bond purchases to inject liquidity into the financial system. This action increased the level of reserves in the banking system, reducing the immediate need for repo operations.
• Standing Facility: Banks can still access liquidity via the RBA’s standing liquidity facility, where they can borrow overnight at a penalty rate if their ESA balances fall short.
• Interbank Cash Market: Banks continue to borrow and lend among themselves in the interbank cash market to manage daily fluctuations in their ESA balances.
• Repo Transactions in the Private Market. While the RBA no longer conducts open market repos, banks and other financial institutions still use repo transactions with each other as a way to manage liquidity and secure short-term funding. These private market repos are similar in structure to the RBA’s past operations but are conducted bilaterally between financial institutions.

Liability-side liquidity and management

• Liability management is closely linked to liquidity management
• Overall aim of liability management: to construct a low-cost and low–withdrawal-risk liability portfolio
• Problems
  • Low-cost liabilities often carry high withdrawal risk: e.g., demand deposits
  • Low withdrawal risk often comes with high cost: e.g., certificates of deposit (CDs)

Liability management (cont’d)

Deposit liabilities

• Cheque account and other demand deposits
• Savings account
• Cash management account (CMA) / investment savings accounts
• Fixed-term deposits
• Negotiable certificates of deposits (NCDs)

Non-deposit liabilities

• Interbank funds
• Repurchase agreements (Repos)
• Covered bonds
• Other borrowings
• Bank accepted bills
• Commercial bills or non-bank bills
• Commercial paper or promissory notes
• Subordinated debt, medium-term notes and long-term borrowings

Sovereign Risk, Foreign Exchange Risk, and Off-Balance-Sheet Risk

Foreign exchange risk

An FI’s overall FX exposure in any given currency can be measured by the net position exposure, which is measured in local currency as

\[ \begin{aligned} \text{Net exposure}_i &= (\text{FX assets}_i - \text{FX liabilities}_i) + (\text{FX bought}_i - \text{FX sold}_i) \\ &=\text{Net foreign assets}_i + \text{Net FX bought}_i \end{aligned} \]

where \(i\) represents the \(i\)th currency.

FX rate volatility and FX exposure

We can measure the potential size of an FI’s FX exposure as:

\[ \begin{aligned} \text{Dollar loss/gains in currency } i &= \text{Net exposure in foreign currency } i \text{ measured in local currency} \\ &\times \text{Shock (volatility) to the exchange rate of local currency to foreign currency } i \end{aligned} \]

• Greater exposure to a foreign currency combined with greater volatility of the foreign currency implies greater daily earnings at risk (DEAR).
• Reason for FX volatility: fluctuations in the demand for and supply of a country’s currency

Interaction of interest rate, inflation, and exchange rates

• Global financial markets are increasingly interconnected, so are interest rates, inflation, and foreign exchange rates.
• We now explore how inflation in one country affects its foreign currency exchange rates, focusing on purchasing power parity (PPP).
• Next, we examine the relationship between domestic/foreign interest rates and spot/forward foreign exchange rates, known as interest rate parity (IRP).

Purchasing Power Parity

Nominal interest rate \(R\) is basically the sum of inflation \(i\) and real interest rate \(r\):

For two countries, e.g., Australia (AU) and United States (US), we have:

\[ \begin{aligned} R_{AU} &= i_{AU} + r_{AU} \\ R_{US} &= i_{US} + r_{US} \end{aligned} \]

Assuming real interest rates are equal across countries: \(r_{AU}=r_{US}\), then

\[ R_{AU} - R_{US} = i_{AU} - i_{US} \]

That is, the (nominal) interest rate spread between Australia and the United States represents the difference in inflation rates between the two countries.

Important

When inflation rates and/or interest rates change, foreign exchange rates (without government control) should adjust to account for relative differences in the price levels (inflation) between the two countries.

The Purchasing Power Parity (PPP) is one theory explaining how this adjustment takes place.

Purchasing Power Parity (cont’d)

Let’s think of an example to illustrate the idea of PPP.

• Imagine you have $1 and can buy one candy in the U.S. Now, let’s say in Japan, 100 yen also buys one candy.
• If $1 is worth 100 yen, things are “balanced”.
• But if candy’s price in Japan increases to 150 yen (inflation in Japan), your $1 won’t buy as much candy anymore.

PPP states that, in different countries, the same money should buy the same amount of goods and services. So, when prices change, the money’s value changes, too, to keep things fair.

• The relative value of money is the exchange rate!

Purchasing Power Parity (cont’d)

Tip

The PPP says that the most important factor determining exchange rates is the price differences drive trade flows and thus demand for and supplies of currencies.

Specifically, the PPP theorem states that the change in the exchange rate between two countries’ currencies is proportional to the difference in the inflation rates in the two countries. That is:

\[ i_{domestic} - i_{foreign} = \frac{\Delta S_{domestic/foreign}}{S_{domestic/foreign}} \]

where

• \(S_{domestic/foreign}\) is the spot exchange rate of the domestic currency for the foreign currency
• \(\Delta S_{domestic/foreign}\) is the change in the one-period spot exchange rate

Purchasing Power Parity (cont’d)

Suppose that the current spot exchange rate of Australian dollars for Chinese yuan, \(S_{AUD/CNY}\), is 0.17 (i.e. 0.17 dollars, or 17 cents is equal to 1 yuan). The price of Chinese-produced goods increases by 10 per cent (i.e. inflation in China \(i_C\), is 10 per cent), and the Australian price index increases by 4 per cent (i.e. inflation in Australia, \(i_{AUS}\), is 4 per cent). What will be the change of the exchange rate?

According to PPP:

\[ i_{AUS} - i_{C} = \frac{\Delta S_{AUD/CNY}}{S_{AUD/CNY}} \]

So that

\[ 0.04 - 0.1 = \frac{\Delta S_{AUD/CNY}}{0.17} \]

Solving the equation, we get \(\Delta S_{AUD/CNY} = −0.0102\). Thus, it costs 1.02 cents less to receive a yuan. The Chinese yuan depreciates in value by 6 per cent against the Australian dollar as a result of its higher relative inflation rate. In other words, a 6 per cent fall in the yuan’s value translates into a new exchange rate of 0.1598 dollars per yuan.

Purchasing Power Parity (cont’d)

The theory behind purchasing power parity is the law of one price, an economic concept which states that in an efficient market, if countries produce a good or service that is identical to that in other countries, that good or service must have a single price, no matter where it is purchased.

Interest Rate Parity

To illustrate (covered) interest rate parity (IRP), let’s consider two investment strategies.

Strategy 1: Domestic Investment

• You invest $1 domestically at an interest rate \(r_d\) for one period.
• After one period, your investment grows to \(1 + r_d\).

Strategy 2: Foreign Investment with Forward Contract

• You convert $1 into foreign currency at the current spot exchange rate \(S\), which gives \(1/S\) foreign currency.
• You then invest the foreign currency amount in a foreign asset at the interest rate \(r_f\) for one period.
• After one period, this investment grows to \((1 + r_f)\).
• You lock in the forward exchange rate \(F\) now to convert the foreign currency back to domestic currency after one period.

For these two strategies to have the same return (and eliminate arbitrage opportunities), the returns on both should be equivalent when the foreign investment is converted back using the forward rate. This gives us the CIRP condition:

\[ 1 + r_d = \frac{(1 + r_f) \cdot F}{S} \]

Rearranging, we can see the relation between interest rates and the forward rate:

\[ F = S \cdot \frac{1 + r_d}{1 + r_f} \]

Managing FX risk

On-balance-sheet hedging

• Requires duration matching to control exposure to foreign interest rate risk
• A direct match of foreign assets and liabilities can result in positive profits for the FI

Off-balance-sheet hedging

• Uses forwards, futures, options and swaps
• Example: hedging with forwards allows FI to offset uncertainty regarding the future spot rate on a currency

Sovereign risk

• Mismatches in the size and maturities of foreign assets and liabilities expose FIs to FX risk.
• Beyond FX risk, holding assets in a foreign country also exposes FIs to country or sovereign risk.
  • e.g., when the foreign corporation may be unable to repay the principal or interest on a loan even if it would like to.
  • the government of the country in which a borrower is headquartered may prohibit or limit debt payments

A sovereign country’s (negative) decisions on its debt obligations or the obligations of its public and private organizations may take two forms: repudiation and restructuring.

1. Debt repudiation
   • An outright cancellation of all a borrower’s current and future foreign debt and equity obligations
2. Debt restructuring
   • Change the contractual terms of a loan, such as maturity and interest payment
   • Most common form of sovereign risk

Off-balance-sheet (OBS) activities

OBS items are “off-balance-sheet” as they appear frequently as footnotes to financial statements.

In economics terms, OBS items are contingent assets and liabilities that affect the future shape of an FI’s balance sheet. They potentially can produce positive or negative future cash flows for an FI.

• The true picture of net worth should include market value of on- and off-balance-sheet activities.

Incentives to increase OBS activities:

• Generate additional income
• Avoid regulatory costs or taxes
  • Reserve requirements
  • Deposit insurance premiums
  • Capital adequacy requirements

Major types of OBS activities

• Loan commitment: Contractual commitment to make a loan up to a stated amount at a given interest rate in the future.
• Letters of credit: Contingent guarantees sold by an FI to underwrite the performance of the buyer of the guaranty.
• Derivative contract: Agreement between two parties to exchange a standard quantity of an asset at a predetermined price at a specified date in the future.
• When-issued trading: Trading in securities prior to their actual issue.
• Loans sold: Loans originated by an FI and then sold to other investors that (in some cases) can be returned to the originating institution in the future if the credit quality of the loans deteriorates.

Role of OBS activities in reducing risk

• OBS activities are not always risk-increasing activities
• In many cases they are hedging activities designed to mitigate exposure to interest rate risk, foreign exchange risk etc.
• OBS activities can decrease an FI’s insolvency risk
• OBS activities are frequently a source of fee income, especially for the largest, most credit-worthy banks

Loan Sales and Securitisation

Loan sales

• The use of credit derivatives allows an FI to reduce credit risk without removing assets from balance sheet.
• With loan sales, a loan is originated by an FI and then sold to an outside buyer (removed from the FI’s balance sheet).
  • There is a transfer of ownership from the seller to the buyer.
  • If a loan is sold without recourse, the FI has no explicit liability even if the loan defaults.
  • If a loan is sold with recourse, the buy may put the loan back to the selling FI under certain conditions.
  • In practice, most loans are sold without recourse.
• Loan sales do not create new types of securities such as the pass-throughs, CMOs, and MBBs, which are products of securitisation.

Types of loan sales

Traditional short-term loan sales

• secured by assets of the borrowing firm.
• made to investment-grade borrowers or better.
• issued for a short term (90 days or less).
• have yields closely tied to the commercial paper rate.
• sold in units of $1 million and up.

Leveraged loan sales

• term loans (TLs).
• secured by assets of the borrowing firm (usually given senior secured status).
• a long maturity (often three- to six-year maturities).
• have floating rates tied to LIBOR, the prime rate, or a CD rate.
• have strong covenant protection.

Note

The definition of “leveraged loan” is ambiguous: some use spreads (e.g., +125bps) and others use rating criteria (e.g., BB- or lower).

Why loan sales?

Apart from credit risk management, there are some other reasons for FIs to sell loans.

1. Reserve requirements (becoming less important)
2. Fee income
3. Capital costs (by reducing risky assets)
4. Liquidity risk (by improving asset-side liquidity)

Securitisation

Asset securitisation is another mechanism to manage credit risk, interest rate risk, liquidity and more.

• It is the process of packaging loans or other assets into newly created securities and selling these asset-backed securities (ABS) to investors.
• Two basic mechanisms of securitisation, but both involve the creation of off-balance-sheet subsidiaries:
  • special-purpose vehicle (SPV, aka special-purpose entity, SPE)
  • structured investment vehicle (SIV)

The mechanism is:

1. The loans are transferred from the originating FI to the SPV or SIV.
2. The SPV or SIV securitizes the loans (either directly or through the issuance of asset-backed commercial paper) and then sells the resulting asset-backed securities to investors.
3. The proceeds of the asset-backed security sale are paid to the FI that originates the loans.

Three major forms of securitisation

The major forms of asset securitisation are:

1. the pass-through security,
2. the collateralized mortgage obligation (CMO), and
3. the mortgage-backed bond (MBB).

Emerging topics in bank risk management

Changing dynamics

• Traditional “banks”, taking deposits and grant loans, are facing increasing challenges.
• Global competition with other banks.
• Competition with nonbanks or “shadow banks”.
  • Many of banks’ functions can be now performed by nonbanks.
  • For example, FinTech firms may better reduce information asymmetry through screening and monitoring based on big data and advanced technologies (AI/ML), improved and customized services, and reduced cost of search and match with platform economy.
  • More importantly, nonbanks are not regulated or less regulated than banks.
• Central bank digital currencies (CBDC).
  • Increased funding costs for banks if households hold CBDC instead of bank deposits.
• Technological advancement.
  • Online/mobile banking simplifies transfer of funds.
• Transition from “originate and hold” to “originate and distribute” business model.

Finally…

References

Broecker, Thorsten. 1990. “Credit-Worthiness Tests and Interbank Competition.” Econometrica 58 (2): 429.

Diamond, Douglas W., and Philip H. Dybvig. 1983. “Bank Runs, Deposit Insurance, and Liquidity.” Journal of Political Economy 91 (3): 401–19.

Freixas, Xavier, and Jean-Charles Rochet. 2023. Microeconomics of Banking. 3rd ed. MIT Press.

Holmstrom, Bengt, and Jean Tirole. 1997. “Financial Intermediation, Loanable Funds, and the Real Sector.” Quarterly Journal of Economics 112 (3): 663–91.

Modigliani, F, and M H Miller. 1958. “The Cost of Capital, Corporation Finance and the Theory of Investment.” The American Economic Review 48 (3): 261–97.

Saunders, Anthony, Marcia Millon Cornett, and Otgo Erhemjamts. 2023. Financial Institutions Management ISE. 11th ed. McGraw Hill.